Зачем математики ищут простые числа, как выглядит самое большое простое число и почему в цифровом мире нам не обойтись без этих знаний.
Простые числа с древности изучают математики всего мира. С ними связана до сих пор не доказанная гипотеза Римана — одна из величайших математических проблем. Простые числа составляют основу современной кибербезопасности, а в будущем, возможно, найдутся гораздо более экзотические способы их применения: так, в научно-фантастическом романе «Контакт» астрофизик Карл Саган описал попытки наладить связь с внеземными формами жизни с помощью передачи простых чисел по радиоволнам. Объясняем, почему простые числа имеют такое значение.
В музыке простые числа объясняют эффекты, вызываемые повторением сложных ритмических рисунков. В биологии есть гипотеза, что цикады эволюционировали таким образом, чтобы находиться в спячке в течение простого числа лет для получения эволюционного преимущества. В криптографических системах свойства простых чисел обеспечивают безопасность электронных коммуникаций. Возможно, в будущем именно простые числа будут использоваться для коммуникации с внеземными формами жизни, так как они независимы от любого представления о языке, и при этом достаточно сложны, чтобы спутать их с результатом природного физического процесса.
Почему простые числа так важно изучать
Простые числа имеют фундаментальное значение для математики. Они являются структурными единицами теории чисел, своего рода «атомами умножения». Это связано с основной теоремой арифметики, которая гласит, что любое число больше единицы можно представить в виде произведения конечного количества простых чисел, причем такое представление единственно. Например, 6=2×3, то есть это произведение двух простых чисел; 20=2×2×5. Поэтому многие проблемы целых чисел могут быть сведены к проблемам простых чисел — точно так же, как некоторые задачи в химии могут быть решены через обращение к атомному составу химических элементов, вовлеченных в систему.
Простое число — это целое число больше единицы, которое делится только на единицу и на само себя. Таким образом, 6 — это не простое число, так как оно может быть представлено как произведение 2×3, а 5 — это простое число, потому что единственный способ представить его как произведение двух чисел — это 1×5 или 5×1. Если у вас есть несколько монет и вы не можете расположить их все в форме прямоугольника, число монет — это простое число. Простых чисел бесконечное множество, и математики пока с трудом ориентируются в нем.https://www.youtube.com/embed/fqI8DyEipXw?rel=0&showinfo=0&autoplay=0
История изучения
Никто точно не знает, когда человечество стало интересоваться простыми числами. Ранних источников, связанных с исследованиями этого математического явления, практически не сохранилось. Скорее всего, древние люди имели какое-то представление о простых числах. Первым реальным доказательством являются египетские записи на папирусах, сделанные более 3500 лет назад.

Древние греки, скорее всего, были первыми, кто стал всерьез изучать простые числа. В частности, древнегреческий математик Евклид доказал существование бесконечного множества простых чисел. Вот его доказательство.
Предположим, есть конечное множество простых чисел, например p1,… pn. Представим, что существует число p1×… ×pn+1 — то есть число, на единицу большее, чем все простые числа из нашего множества, умноженные друг на друга. Очевидно, что это число не может быть произведением любых чисел ряда p1,… pn и оно больше 1. Поэтому оно должно делиться на некое простое число, не включенное в этот набор. Добавляя новые простые числа в этот список и повторяя те же действия, всегда можно найти по крайней мере одно новое простое число. Поэтому должно существовать бесконечное множество простых чисел.
После греков серьезное внимание простым числам уделили только в XVII веке. В 1637 году французский математик Пьер де Ферма сформулировал великую теорему Ферма: уравнение xn+yn=zn не имеет натуральных решений при n>2. Эта проблема связана с простыми числами. Лишь в 1994 году американскому математику Эндрю Уайлсу удалось доказать великую теорему Ферма.
В XVIII веке много теорем, связанных с простыми числами, доказал Леонард Эйлер. Его работа в теории чисел включала в себя множество сведений о простых числах. Эйлеру и Лейбницу удалось доказать так называемую малую теорему Ферма: если p — простое число и a — целое число, не делящееся на p, то ap-1–1 делится на p. Она оказалась частным случаем теоремы Эйлера.
Кроме того, Эйлер опроверг предположение Ферма о том, что все числа вида Fn=22n+1 простые. Эйлер также показал, что бесконечный ряд ½+1/3+1/5+1/7+1/11+… является расходящимся, то есть сумма этих дробей равна бесконечности. И, наконец, в переписке с Эйлером математик Христиан Гольдбах сформулировал знаменитую гипотезу Гольдбаха о представлении любого четного числа начиная с 4 в виде суммы двух простых. Эта гипотеза до сих пор не доказана.
В XIX веке большой прорыв был сделан благодаря Карлу Фридриху Гауссу, Пафнутию Чебышёву и Бернхарду Риману, особенно в отношении распределения простых чисел.
Кульминацией стала до сих пор не решенная гипотеза Римана, которую часто называют важнейшей нерешенной задачей всей математики. Она позволяет очень точно предсказать появление простых чисел, а также отчасти объясняет, почему они даются математикам с таким трудом.
Распределение простых чисел по Гауссу
Если посмотреть на распределение простых чисел, можно заметить кое-что интересное: чем дальше вы продвигаетесь по числовой прямой, тем реже и реже встречаются простые числа, хотя точную закономерность установить сложно. Например, есть четыре простых числа меньше 10; 25 простых чисел меньше 100; 168 простых чисел меньше 1000. Таким образом, пропорция простых чисел до 10 равна 0,4, пропорция простых чисел до 100 — 0,25, а до 1000 — 0,168: чем больше числа, тем меньше среди них простых чисел, хотя множество простых чисел бесконечно.
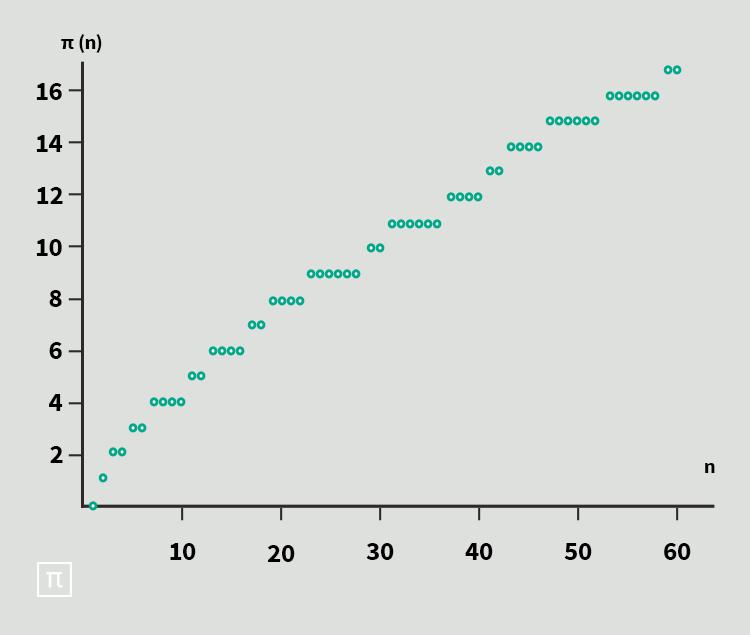
Функция распределения простых чисел, или пи-функция (с числом π никак не связана), равняется числу простых чисел, меньших либо равных действительному числу x
В 1790-х годах Гаусс, который тогда еще учился, строил огромные таблицы простых чисел. Он обнаружил, что плотность распределения простых чисел на отрезке [1; n] приблизительно равна 1/ln n. Если вы не знаете, что такое натуральный логарифм ln n, это не так важно: в данном случае про него вам нужно знать то, что он растет с увеличением n, но все медленнее и медленнее. Если вы хотите получить примерное представление, ln n очень приблизительно равен числу разрядов (то есть количеству цифр) в n, умноженному на два. Это значит, что плотность распределения простых чисел медленно, очень медленно стремится к нулю. Гаусс предположил, что это будет верно для любых целых n, а не только для тех, которые он рассчитал, однако доказать это не смог.
Доказательство нашли в 1896 году независимо друг от друга два математика — Жак Адамар и Шарль Жан де ла Валле-Пуссен. Средняя разность между некоторым простым числом p и следующим простым числом приблизительно равна ln p. Она может быть маленькой, например всего 2, а может быть сколь угодно большой, но в среднем она равна ln p.
Гипотеза Римана
Итак, плотность распределения простых чисел на отрезке [1; n] «приблизительно равна 1/ln n». Но это неточная оценка, и необходимо понять насколько. В середине XIX века решить этот вопрос попытался Бернхард Риман. Он использовал так называемую дзета-функцию Римана.
На самом деле дзета-функцию ввел Леонард Эйлер в 1730-х годах. Он доказал, что ее можно представить как бесконечное произведение, где сомножители — это результат вычислений по определенной формуле для каждого из простых чисел. Именно эта связь с простыми числами (понимание поведения этой функции) дает нам некоторое представление о распределении простых чисел.
Риман расширил определение этой функции от только вещественных чисел до комплексных чисел, и это позволило ему связать распределение простых чисел с нулями функции, то есть с теми числами, при которых функция принимает нулевое значение. Какие-то нули функции очевидны для математиков (это отрицательные четные целые числа –2, –4, –6), но поиск других требует определенных усилий. Риман вычислил несколько таких нетривиальных корней и заметил, что у них всех есть что-то общее: все они выглядят как ½+it, где i — квадратный корень из отрицательного числа, а t является действительным числом (то есть его можно изобразить на числовой прямой). Эти комплексные числа, при которых функция принимает нулевое значение, нельзя изобразить на числовой прямой, но можно показать на координатной плоскости: область значений нетривиальных нулей функции будет выглядеть как вертикальная линия (на рисунке — критическая линия).
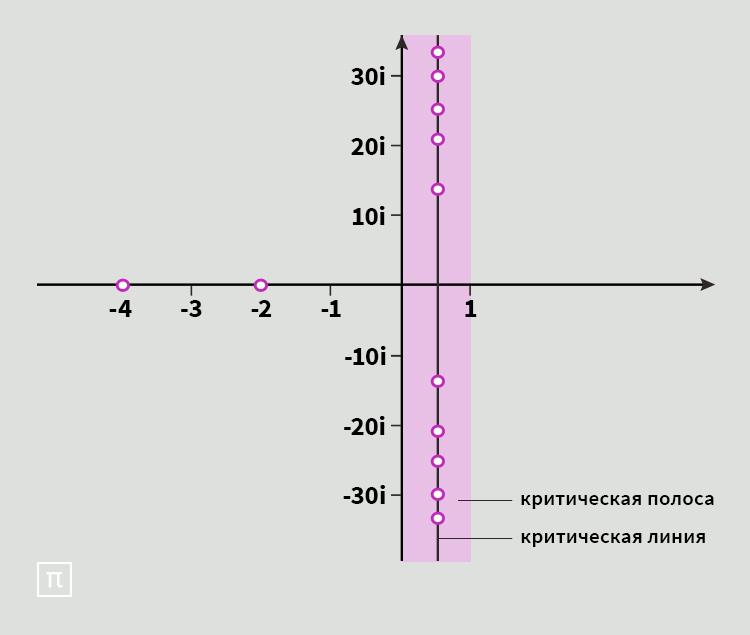
В чем заключается сама гипотеза Римана? Существуют только те нули дзета-функции, о которых мы знаем, и никаких иных нулей функции нет. Если это можно будет доказать, то мы получим намного больше знаний о том, насколько точно 1/ln n описывает распределение простых чисел на отрезке [1; n], и это поможет математикам с другими аналогичными оценками в теории чисел.
Выведя теорему о распределении простых чисел, Жак Адамар и Шарль-Жан де ла Валле Пуссен доказали, что все нетривиальные нули дзета-функции лежат в пределах критической полосы (указана на графике). Доказательства у обоих получились очень сложными и техничными, но тем не менее свою задачу они выполнили. Однако сама по себе гипотеза Римана по-прежнему остается недоказанной.
Гипотеза Римана, выдвинутая 160 лет назад, до сих пор считается одной из самых важных и престижных открытых проблем математики. В 2000 году Математический институт Клэя объявил семь задач, за решение каждой из которых математикам предлагалась награда в миллион долларов. Одна из них спустя несколько лет была решена: математик Григорий Перельман доказал гипотезу Пуанкаре (и это, пожалуй, величайшее достижение математики XXI века). Оставшиеся шесть проблем остаются открытыми, включая гипотезу Римана.
Поиск новых простых чисел
Леонард Эйлер доказал, что число Мерсенна (231)−1=2147483647 — простое число, и до 1867 года оно оставалось наибольшим известным простым числом. На 2020 год наибольшее известное простое число — 282 589 933−1. Его десятичная запись имеет длину 24 862 048 цифр. Это число было найдено в 2018 году в рамках проекта добровольных распределенных вычислений GIMPS.
Один из способов нахождения простых чисел — компьютерный поиск. Путем многократной проверки того, является ли число множителем 2, 3, 4 и так далее, можно легко определить, простое ли оно. Если оно не является множителем любого меньшего числа, оно простое. Но это очень трудоемкий способ, есть и более эффективные методы. Эффективность этих алгоритмов (или тестов простоты) для каждого числа является результатом теоретического прорыва 2002 года. Было доказано, что задача определить то, является ли данное число простым, полиномиально разрешима. В частности, был разработан первый детерминированный полиномиальный тест простоты — тест Агравала — Каяла — Саксены. С теоретической точки зрения этот тест очень важен, так как он может работать со всеми числами, а не только с числами, обладающими определенными свойствами. Но на практике применять его не очень удобно.
Простых чисел довольно много, поэтому, если взять просто большое число и прибавить к нему единицу, можно наткнуться на простое число. В действительности многие компьютерные программы полагаются на то, что простые числа не слишком трудно найти. Если вы наугад выберете стозначное число, ваш компьютер найдет следующее за ним простое число за несколько секунд.
Как правило, математики не ищут отдельные простые числа на компьютере. Но они очень заинтересованы в простых числах с особыми свойствами. Есть две известные проблемы: существует ли бесконечное количество простых чисел, которые на один больше, чем квадрат (например, это имеет значение в теории групп), и существует ли бесконечное количество пар простых чисел, отличающихся друг от друга на 2.
Тайны простых чисел
Несмотря на то что простые числа изучаются уже более трех тысячелетий и имеют простое описание, о них до сих пор известно на удивление мало. Например, математики знают, что единственной парой простых чисел, отличающихся на единицу, являются 2 и 3. Однако неизвестно, существует ли бесконечное количество пар простых чисел, отличающихся на 2. Предполагается, что существует, но это пока не доказано. Это проблема, которую можно объяснить ребенку школьного возраста, однако величайшие математические умы ломают над ней голову уже более 100 лет.
Многие из наиболее интересных вопросов о простых числах как с практической, так и с теоретической точки зрения заключаются в том, какое количество простых чисел имеет то или иное свойство. Ответ на самый простой вопрос — сколько есть простых чисел определенного размера — теоретически можно получить, решив гипотезу Римана.
Существуют способы предположить, каким будет правильный ответ на многие из этих вопросов. Догадки математиков подтверждаются численными экспериментами, и есть теоретические основания полагаться на них. Но для чистой математики и работы компьютерных алгоритмов чрезвычайно важно, чтобы эти догадки действительно были верными, и математики могут быть полностью удовлетворены, только имея неоспоримое доказательство, а для гипотезы Римана его пока нет.
Самым серьезным вызовом для практического применения является сложность нахождения всех простых множителей числа. Если взять число 15, можно быстро определить, что 15=5×3. Но если взять 1000-значное число, вычисление всех его простых множителей займет больше миллиарда лет даже у самого мощного суперкомпьютера в мире. На сложности таких вычислений основаны многие алгоритмы защиты данных, поэтому для безопасности коммуникации важно знать, что никто не придумает быстрый способ находить простые множители у больших чисел.
Применение простых чисел в будущем
Сейчас невозможно сказать, как простые числа будут использоваться в будущем. Для теорий, которые разрабатывались в чистой математике, неоднократно находились самые неожиданные применения. Снова и снова идеи, воспринимавшиеся как причуды математиков, оказывались на удивление полезными для науки и техники. В начале XX века математик Годфри Харольд Харди утверждал, что простые числа не имеют реального применения, но уже 40 лет спустя стал очевиден их потенциал для компьютерной коммуникации, и сейчас без них невозможно повседневное использование интернета.
Поскольку простые числа лежат в основе проблем, касающихся целых чисел, а целые числа постоянно встречаются в реальной жизни, простым числам найдется повсеместное применение в мире будущего. Это особенно актуально, учитывая, что интернет и другие компьютерные технологии играют все большую роль в нашей жизни.Все простые числа относятся к натуральным — тем, которые мы используем в обычной жизни для обозначения предметов. Однако множество натуральных чисел входит в другое множество — в действительные числа, которые представляют собой множество всех чисел на непрерывной числовой прямой. Кроме того, математики оперируют и другими множествами чисел, например комплексными. Как вам кажется, какое из этих утверждений не относится к числам вообще?Про действительные числа можно думать как про некоторые операции, которые мы производим над точками прямойКомплексные числа можно интерпретировать геометрически, их можно отождествить с точками плоскостиГиперкомплексные числа Гамильтона — кватернионы — можно представить как трехмерные векторы, обладающие мерой вращения вокруг своей осиТрехмерные гиперкомплексные числа представимы в виде трехмерных векторов в трехмерном пространстве
Литература
Г. Диамонд, Элементарные методы в изучении распределения простых чисел, УМН, 1990, том 45, выпуск 2(272), 79–114
Главы | Закономерности простых чисел. Гипотеза Римана
История функционального уравнения дзета-функции и роль различных математиков в его доказательстве — лектор Я. В. Благушин
Доказательство гипотезы Пуанкаре (по работам Г. Перельмана)
Полное доказательство гипотезы Пуанкаре предъявлено уже тремя независимыми группами математиков
Графики — Андрей Носков
Источник: postnauka.ru

